El sistema en base 10 (sistema Decimal) tiene como cifras disponibles desde el 0 hasta el 9, y el valor de posición es una potencia de 10. Así, el número 13 lo podemos escribir de la siguiente manera:

Sin embargo, aunque el sistema decimal es muy fácil de usar por los humanos, los ordenadores se las entienden mejor utilizando el sistema en base 2 (sistema Binario), en cuya base las cifras disponibles son el 0 y el 1, y el valor de posición es una potencia de 2.

El número 13 en el sistema binario se obtiene de la siguiente manera: se divide el número 13 entre 2 obteniéndose 6 de cociente y 1 de resto. El cociente (6) lo volvemos a dividir entre 2 y obtenemos 3 de cociente y 0 de resto. Seguimos este proceso dividiendo los sucesivos cocientes entre 2 y el proceso se acaba cuando obtengamos un cociente cuyo valor sea 1. Las cifras que componen el número 13 en el sistema binario se escriben comenzando por la correspondiente al último cociente obtenido (siempre será un 1) y siguiendo por las correspondientes a los sucesivos restos de las divisiones comenzando por el resto obtenido en la última división y finalizando por el resto obtenido en la primera división. De esta manera el número 13 se escribe como 1101 en el sistema binario.

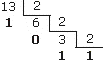
Una de las desventajas de la numeración binaria es que requiere números relativamente largos y que resultan confusos para ser manejados por personas. Para facilitar este manejo, se ha recurrido al sistema de numeración en base 16 o Hexadecimal. En base 16 disponemos de 16 cifras: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, y F (las letras tienen los valores decimales de 10 en adelante) y el valor de posición es una potencia de 16. De hecho, 16 es una potencia de 2 (2⁴).

Los números binarios de cuatro cifras (desde 0 a 1111 que corresponden a los números en el sistema decimal desde el 0 al 15) se pueden representar con una sola cifra hexadecimal. Esto hace que sean más fáciles de leer para los humanos y más fácil operar con ellos. Con la práctica, es relativamente fácil memorizar las equivalencias entre números binarios y hexadecimales y convertir entre uno y otro sistema sin dificultades con una tabla como la siguiente:

La numeración hexadecimal es frecuente en todo lo referente a la imagen digital. Los colores Rojo (Red), Verde (Green) y Azul (Blue) (RGB) se suelen especificar mediante un código hexadecimal de 6 cifras. Cada par de cifras, de izquierda a derecha, representa el componente de color Rojo (cifras 1ª y 2ª), Verde (cifras 3ª y 4ª) y Azul (cifras 5ª y 6ª). Cada uno de los componentes puede adoptar 256 niveles, desde 00 (mínimo de color) hasta FF (máximo de color). El color negro se representa por 000000, el color blanco por FFFFFF, el color azul puro se representa por 0000FF, el color verde puro por 00FF00 y el color rojo puro por FF0000. Un amarillo muy claro es FFFFCC, o sea, que el rojo y el verde están al máximo y el azul bastante alto, lo que da un resultado próximo al blanco FFFFFF.

La ventaja de utilizar el sistema hexadecimal es lo fácil que resulta de leer el número y distinguir el peso de cada componente. De esta manera, el total de colores que se pueden representar así es de:

Todo lo anterior lo podemos representar mediante el siguiente esquema:

Una imagen digital se compone de puntos o píxeles dispuestos en filas y columnas. En función del tipo de imagen digital, el punto puede ser blanco o coloreado.

La calidad de una imagen depende del número de puntos utilizados para crearla. Este valor se conoce como resolución de la imagen digital. La resolución se mide en puntos por pulgada (ppp) y refleja simplemente el número de puntos utilizados para componer una imagen. Por ejemplo, en una imagen con una resolución de 300 ppp, cada pulgada de la imagen (una pulgada son 2,54 cm) contiene 300 puntos. Dicho de otro modo, cada punto o píxel que compone la imagen ocupa 1/300 de pulgada. Esto implica que una imagen de baja resolución (por ejemplo, 50 ppp) puede aparecer moteada, mientras que es probable que una imagen de mayor resolución tenga una apariencia correcta.

Una imagen de color auténtico o verdadero es una imagen de 24 bits (3 x 8 bits = 24 bits) compuesta de puntos rojos, verdes y azules, cada uno de los cuales puede mostrar un valor entre 256 posibles. Una imagen digital de color auténtico es lo más parecido a una imagen de calidad fotográfica, ya que puede mostrar un color entre de tonos posibles .

Los números binarios de una sola cifra no aportan mucha información ya que sólo pueden informar de la presencia o ausencia de algo. A cada cifra binaria la llamamos Bit (palabra que supuestamente es una abreviatura del inglés binary digit, o sea, dígito binario). Necesitamos varias cifras binarias para representar un mayor número de estados.

Un bit (b) es la unidad mínima de información empleada en informática, en cualquier dispositivo digital, o en la teoría de la información. Con él, podemos representar dos valores cualquiera, como por ejemplo: verdadero o falso, abierto o cerrado, apagado o encendido, blanco o negro, norte o sur, masculino o femenino, amarillo o azul, etc. Basta con asignar cada una de las cifras (0 ó 1) a cada uno de los estados.

Un Byte (B) es un conjunto de bits (unos y ceros) de longitud específica que equivale a un valor en la codificación de un ordenador. El término Byte tiene generalmente un valor de ocho bits (octeto) y puede almacenar un número entero entre

 Con 16 cifras (o bits) obtendríamos

Los bytes comenzaron a usarse como unidades básicas a la hora de hablar de capacidad de un ordenador, ya fuera refiriéndose a la memoria o al almacenamiento en disco de los archivos. Cada byte puede representar un carácter (letra, número, signo de puntuación) o un carácter de control (espaciador, final de línea, etc). Un carácter tendrá una cantidad de 8 bits, que es igual a decir que ocupa un byte de memoria. Todos los caracteres que escribimos a través del teclado del ordenador son procesados por un circuito “traductor” (codificador o descodificador) que los convierte en lenguaje binario y viceversa. Tal circuito busca las equivalencias en una tabla de filas y columnas que hace las veces de un diccionario para traducir palabras de un idioma a otro. Hasta hace poco, las tablas más utilizadas eran la ASCII y la ANSI, con capacidad para 256 caracteres, pero en la actualidad han sido desplazadas por la tabla UNICODE, con capacidad para 65536 caracteres. Un carácter tendrá una cantidad de 8 bits, que es lo mismo que decir que ocupa un byte de memoria.

Sin embargo, es necesario utilizar unidades de orden superior ya que hasta un texto relativamente breve puede ocupar varios miles de bytes. La unidad de orden superior utilizada en primer lugar fue el Kilobyte (KB), equivalente a 1.024 bytes ó 210 bytes.  La siguiente unidad de orden superior fue el Megabyte (MB), equivalente a 220 bytes, o lo que es lo mismo, 1024 KB. En la actualidad lo habitual es hablar de capacidades del orden de los Gigabytes (GB), que equivalen a 230 bytes, o sea, 1024 MB y ya se comienza a hablar de capacidades del orden de los Terabytes (TB), que equivalen a 1024 GB.

Los prefijos Kilo, Mega, Giga, Tera, etc. se consideran potencias de 1024 en lugar de potencias de 1000. Esto es así porque 1024 es la potencia de 2 (exponente 10) más cercana a 1000. Kilo viene del griego χίλιοι que significa mil, Mega viene del griego μέγας que significa gran, Giga viene del griego γίγας que significa gigante y Tera viene del griego τέρας que significa monstruo. En el año 1998, el IEC (Comisión Internacional de Electrotecnia) creó un nuevo sistema de prefijos para referir múltiplos binarios. El padrón de prefijos del IEC especifica que los prefijos del S.I. (sistema internacional de unidades) deben usarse únicamente para múltiplos en base 10, y no en base 2.

La velocidad de transmisión de datos es simplemente el número de bits transmitidos por segundo (bps) cuando se envía un flujo continuo de datos, y el Ancho de Banda expresa la cantidad máxima de datos que pueden ser transmitidos en un tiempo determinado (en las redes se expresa en bps).

Para poder enviar y recibir datos necesitamos un módem. La palabra módem proviene de la contracción de los términos modulador y demodulador, lo que da idea de las funciones que lleva a cabo el equipo: transforma las series de unos y ceros, que proporciona el ordenador para transmitir, en señales de tipo analógico, aptas para viajar por los cables o líneas telefónicas, y viceversa. Para que una transmisión de datos sea posible es preciso que exista un módem en cada uno de los extremos de la línea, conectado a los terminales u ordenadores existentes, y que todos los módems sean compatibles es decir, que procedan de la misma forma con los datos.

El almacenamiento o tamaño de los archivos se especifica en bytes (Kilobytes, Megabytes, Gigabytes, etc.). Sin embargo, muchos equipos de comunicación (módems, routers, etc.) y los navegadores o los programas de descarga de archivos especifican la velocidad en kilobytes por segundo, creando bastante confusión entre los usuarios.

Cada byte se compone de 8 bits, que son la unidad mínima de información (un 0 ó un 1). Así, para convertir kilobits a kilobytes no hay más que dividir por 8, lo mismo que habría que hacer con las velocidades de transmisión: 256 kbits por segundo equivalen a 32 Kbytes por segundo. Con esa velocidad de transmisión de datos, para descargar un Megabyte hay que emplear 32 segundos, sin olvidar que un Megabyte son 1.024 Kilobytes

Si contratamos una conexión ADSL de 1 Mb (1024 kps / 300 kbps) sucede lo siguiente:

el ordenador recibirá datos (descarga) a una velocidad máxima de

y los enviará (subida) a una velocidad máxima de

cifras que además nunca se alcanzarán porque los protocolos de transmisión de información de Internet necesitan transmitir datos internos además de los datos "reales" que tú recibes o transmites. Para aproximarse más al rendimiento real de una conexión, se suelen dividir los Kilobits entre 9 e incluso entre 12, siendo 10 la media más aceptada. En general, una regla bastante acertada para calificar de buena una conexión a Internet mediante ADSL es que alcance con regularidad el 80% de la velocidad máxima.

Si contratamos una línea ADSL de 2 Mb (2048 kps / 300 kbps) el proceso es equivalente, es decir:

el ordenador recibirá datos (descarga) a una velocidad máxima de

y los enviará (subida) a una velocidad máxima de

Si, por ejemplo, un archivo se está descargando a 25 KB/s, quiere decir que se están descargando

es decir 25600 caracteres cada segundo. Actualmente, las ofertas de conexión a internet por cable o ADSL varían

 desde 1 Mb en adelante.

Un disco duro de 200 GB puede contener hasta 200 Gigabytes de datos.