Dibujamos un cuadrado de lado 2 unidades y unimos el punto medio de uno de sus lados con uno de los vértices del lado opuesto. Con un compás, llevamos esa distancia sobre el lado inicial y así obtenemos el lado mayor del rectángulo cuyo valor es 

La razón entre el lado mayor del rectángulo y el lado menor es el número áureo o número de oro.

Según el diccionario María Moliner una espiral es una "Línea curva desarrollada en un plano alrededor de un punto del cual se aleja gradualmente, de modo que no llega a cerrarse."

En 1525, el pintor renacentista Alberto Durero (1471-1528) publica una obra titulada Instrucción sobre la medida con regla y compás de figuras planas y sólidas. Es un libro en el que explica diversos métodos para trazar diferentes figuras geométricas, de las cuales la más famosa es una espiral a la que se le ha dado el nombre de Espiral de Durero.

Para su construcción dibujamos un cuadrado de 2 unidades de lado y a partir de él construimos un rectángulo áureo. Pegado al lado mayor del rectángulo áureo dibujamos un cuadrado de lado el lado mayor del rectángulo. Aparece de nuevo un rectángulo áureo, en el cual volvemos a pegar un cuadrado de lado el lado mayor del rectángulo áureo y así sucesivamente.

Si dividimos entre sí los lados mayores de los rectángulos áureos que van apareciendo vemos que en todas las divisiones aparece el número de oro.

Una vez construida esta sucesión de rectángulos áureos encajados, si unimos mediante un arco de circunferencia dos vértices opuestos de cada uno de los cuadrados obtenidos, utilizando como centro de la misma otro de los vértices del mismo cuadrado, obtenemos una curva llamada Espiral de Durero. En realidad esta curva no es una espiral puesto que está formada por arcos de circunferencia pegados. Es una aproximación de una espiral logarítmica.

Leonardo de Pisa, Fibonacci, es conocido sobre todo por una curiosa sucesión de números en la que cada término es la suma de los dos anteriores.

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ...............

Si dividimos dos términos consecutivos de la sucesión de Fibonacci, siempre el mayor entre el menor, obtenemos, al tomar cada vez más términos, el número de oro.

Para dibujar la espiral de Fibonacci comenzamos dibujando dos pequeños cuadrados de lado una unidad, que estén unidos por uno de sus lados. A partir de ahí se forma un rectángulo, cuyo lado mayor, que es 2, sirve como lado de un nuevo cuadrado que unimos a los anteriores. Nuevamente obtenemos un rectángulo de dimensiones 3 x 2 y a partir de aquí, el proceso se reitera sucesivamente añadiendo cuadrados cuyos lados son los números de la sucesión de Fibonacci ya que cada cuadrado tiene como lado la suma de los lados de los dos cuadrados construidos anteriormente.

Esta curva es una aproximación de la llamada espiral equiangular o espiral logarítmica que fue descrita por primera vez por Descartes. Es una aproximación, ya que no puede dibujarse solo con regla y compás. La espiral equiangular o logarítmica tiene una propiedad similar a la de la circunferencia, es decir, que la tangente en cada punto corta al radio vector siempre con el mismo ángulo, de ahí el nombre de equiangular y además los ángulos alrededor del polo son proporcionales al logaritmo del radio vector, de ahí su segundo nombre de espiral logarítmica.

Esta espiral también recibe el nombre de espiral geométrica, ya que mientras el ángulo de giro crece en progresión aritmética, sumando siempre la misma cantidad, el radio correspondiente crece en progresión geométrica, multiplicando siempre el radio anterior por un mismo número.

La espiral logarítmica es el único tipo de espiral que mantiene su forma al ser reescalada y aumenta su tamaño en cada cuarto de vuelta en aproximadamente 1.618034 veces el tamaño anterior. Esta cifra corresponde al número de oro que es el número asociado a la sucesión de Fibonacci.

La siguiente imagen es la de una concha, conocida en los arrecifes de coral del sur del Pacífico como Nautilus pompilius, cuyo corte transversal revela una línea de nácar que forma una perfecta espiral. Este fósil viviente, que al igual que otros cefalópodos se alimenta de peces, crustáceos y carroña, comida que detecta a través del olfato, es una especie nocturna que, aunque trabaja cerca de la superficie, puede habitar a 500 metros de profundidad y, cosa inusual, vivir hasta 20 años. Si damos un corte transversal a la concha veremos que está formada por compartimentos separados por tabiques y comunicados por un sifón. El animal ocupa el compartimento más externo, que es de mayor tamaño. Al ir creciendo el molusco abandona el compartimento anterior y crea uno con la misma forma pero más grande y lo hace de tal manera que sus cámaras aumentan de tamaño pero su forma es invariable.

Las sucesivas vueltas van aumentando en anchura, en proporción constante e invariable. Y esto es precisamente lo que define a las espirales, o al menos a uno de sus tipos, las espirales logarítmicas. Su borde exterior describe una curva que es siempre igual a sí misma.

Existe otra espiral basada en el número áureo que se construye a partir de un triángulo isósceles de ángulos 36º, 72º y 72º. Se comienza trazando la bisectriz de uno de los dos ángulos iguales, por ejemplo el ángulo A, que corta a uno de los lados iguales en el punto D. Se forma así un nuevo triángulo ADC que es semejante al anterior. Si repetimos el proceso trazando la bisectriz del ángulo ACD que corta al lado AD en el punto E se vuelve a formar otro triángulo isósceles ACE que es semejante a los anteriores. Al repetir el proceso indefinidamente, los triángulos que se van formando son todos semejantes y verifican que los cocientes entre el lado mayor y el lado menor de cada triángulo tienden hacia el número de oro, de ahí el nombre de triángulos áureos.

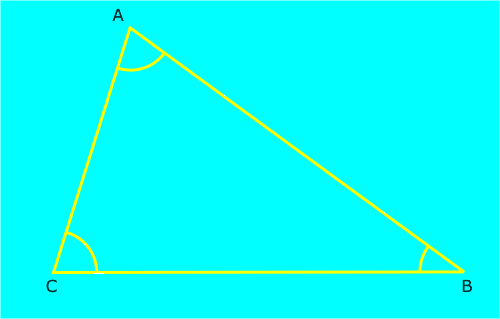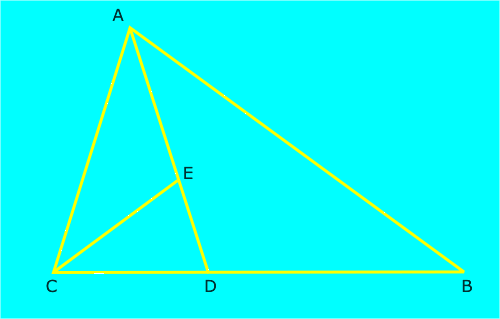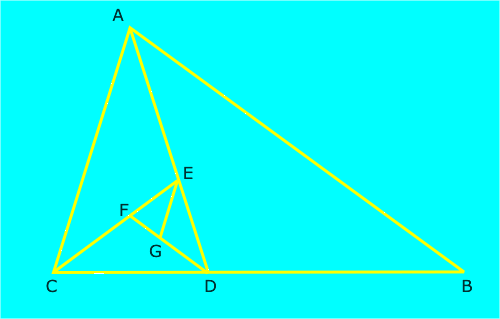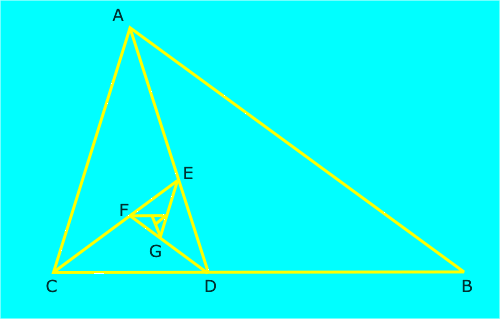
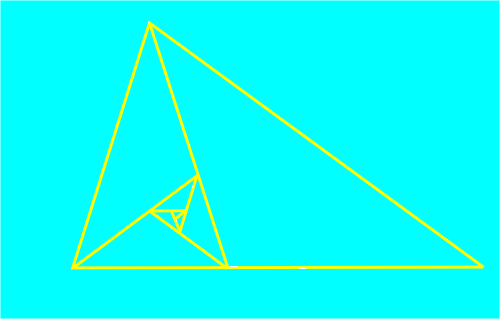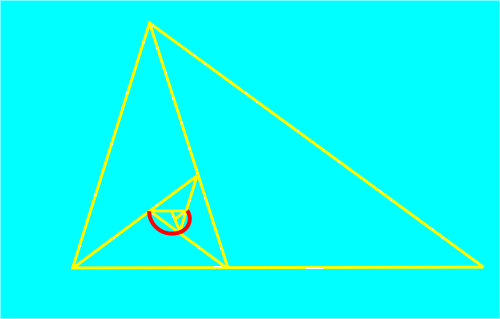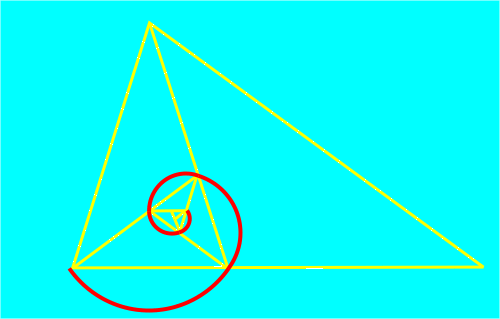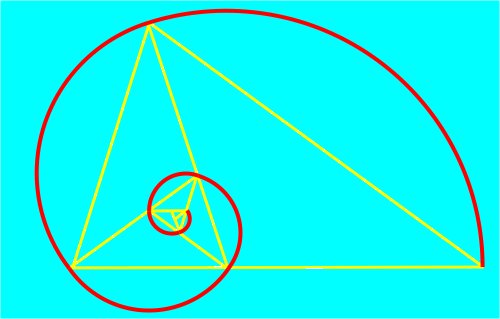
La espiral se construye uniendo mediante arcos de circunferencia los vértices consecutivos de estos triángulos. Los sucesivos arcos que componen la espiral se dibujan tomando como centro el vértice correspondiente al ángulo mayor de cada uno de los triángulos isósceles y como radio la longitud del lado menor.  Esta espiral aumenta su tamaño en cada cuarto de vuelta, en aproximadamente 1.618034 veces el tamaño anterior, es decir que el factor de crecimiento es el número áureo.